Edge detection
www.kovalevsky.de, last update: October 26, 2011
 Let me know
Let me knowwhat you think
| Home | Index of Lectures | << Prev | Next >> | PDF Version of this Page |
Edge detectionwww.kovalevsky.de, last update: October 26, 2011 |
 |
 Let me know
Let me knowwhat you think |
|
|
High-pass filter belong to the eldest known means for edge detection. Filters having been presented in Lecture 1 are low-pass
filters: they suppress the higher spatial frequencies, including the noise; while letting through the lower frequencies. A high-pass
filter makes the opposite. Therefore, it essentially increases the noise. Before applying a high-pass filter, the noise in the image
must be suppressed.
One of the classical edge detecting filter is the Sobel filter. It is defined by two weight matrices:
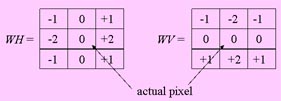 | The filter computes two sums SH and SV of the products of the grey values in the gliding 3x3 neighborhood of the actual pixel with the corresponding weights from the matrices and returns for each actual pixel the sum of the absolute values |SH |+|SV |. The new image thus obtained can be thresholded. The result looks like thick white stripes along the edges of homogeneous regions of the original image. This results are mostly not satisfactory because the edges are too thick (see the figure below). |
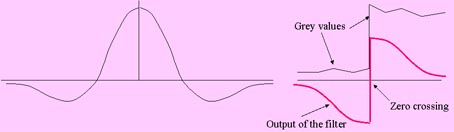
| One of the most efficient edge detectors is the mexican hat filter. It is a high-pass filter. The weights are
distributed in the gliding window as shown in the figure below. The filter computes a new image which contains great positive values on one side of each steep edge in the original image. On the other side there are great negative values. The location where the computed values cross the horizontal line corresponding to zero values corresponds exactly to the location of the edge in the original image. Detecting the zero crossings makes it possible to produce thin lines representing the edges. The lines can be approximated by polygons or subdivided into digital straight segments thus making the analysis of shapes possible. |
 |
 |
 |
Edges are mainly used for analyzing the shapes and sizes of certain parts of the image. For this purpose they must be encoded
"geometrically", i.e. by means of coordinates of points specifying the location and the shape of the edges. There are at
least three methods of geometrically encoding the edges: the crack code, the DSS sequence and the polygonal approximation. The later
two can be produced from the crack code.
The crack code is similar to the well-known chain code with the difference that crack code contains the directions of cracks rather
than that of pairs of pixels.
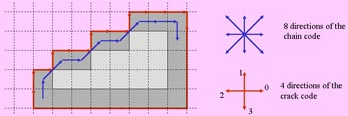 | The crack code can be produced during
the tracing of an edge or of the boundary of a region. It contains the coordinates of the starting point SP, the number
NC of cracks and the sequence of directions DIR. The crack code of the above image: SP=(1,0); NC =26; DIR={1,1,0,1,0,0,1,0,0,1,0,0,0,3,3,3,3,3,2,2,2,2,2,2,2,2}. |
| top of page: |