The definition of the curvature of a curve
The curvature radius R: The limit of the radius of a circle running through three points of the curve, when the distance between
the points tends to zero. The curvature C = 1/R.
Why are the most methods of estimating the curvature imprecise ?
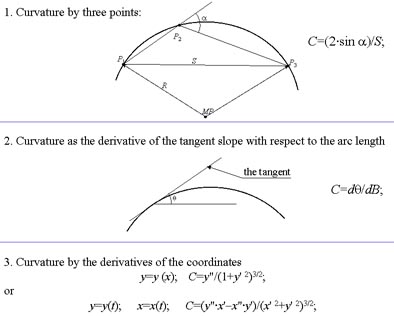The curvature of a curve in a 2D space is defined in analytical geometry by means of derivatives of the function describing the
curve. In digital images curves are defined in a grid. The function describing a curve takes discrete values, e.g. integer values.
How can one compute derivatives of such functions ?
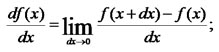 | | Consider the definition of the first derivative of a function of a single variable: |
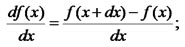 | | What will happen, if we
try to compute the value by the computer while taking dx equal to the smallest number representable in the computer ? |
Numerical calculation of derivatives
| An attempt to estimate the derivative of y=x2 as dy/dx with the smallest
possible value of Δx. | | |
| Looks well | 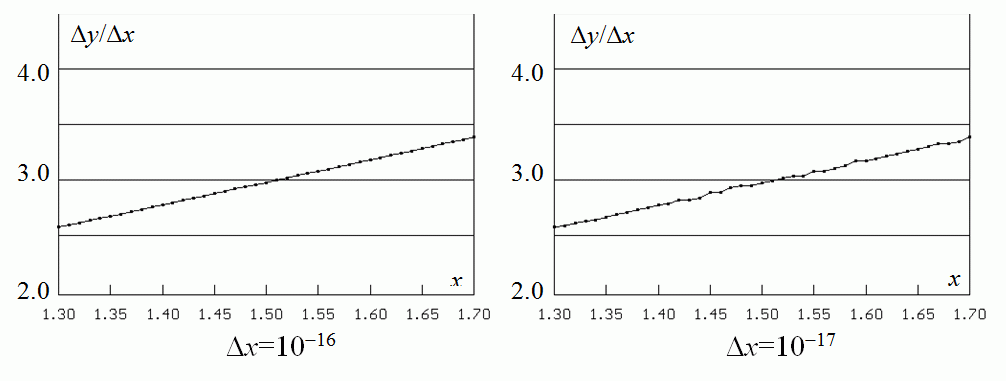 | Small distortions |
| Large distortions | 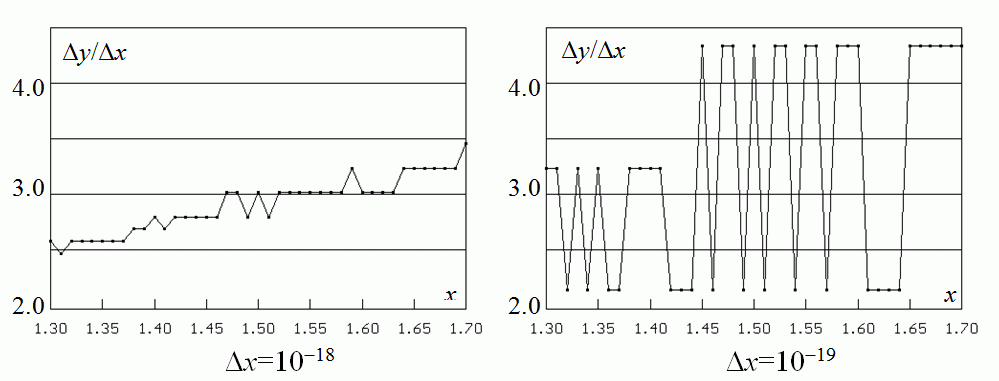 | Crasy values |
The reason of the errors is the limited precision of calculating the values of the function. As soon as the value Δx becomes
less than the error of the function, the brake Δy/Δx obtains senseless value. There is an optimal value of Δx depending
on the magnitude of the extimate of the errors of the function.
Optimal numerical estimates of derivatives: The first derivative
The estimate of the first derivative
E1 = (f(x+Δx)−f(x−Δx)/
(2*Δx);
The values of f(x) cannot be computed exactly; they contain a computation error of ε. We consider the values of
f(x+Δx)+ε, f(x−Δx)+ε and represent
f(x+Δx) and f(x−Δx by the Taylor formula.
E1= [f(x)+f '(x)*Δx +
0.5*f "(x)·Δx2+(1/6)·f (3)
(x+k*Δx)*Δx3−
f(x)−f '(x)*Δx +
0.5*f "(x)·Δx2−(1/6)·f (3)
(x+k*Δx)*Δx3−
where k,m∈[0, 1], F3 is the average value of the third derivative of f(x) in the interval
(x−Δx, x+Δx) and ε is the estimate of the possible error of computing
the values of f(x).
The error Er of the estimation E1:
Er = (1/6)*F3*Δx2 + ε/Δx;
(1)
We find the optimal value of Δx while setting the partial derivative of (1) with respect to Δx equal
to 0 and receive:
optim Δx = (3*ε/F3)1/3;
minimum Error = ((1/6)*32/3+3-1/3)*
ε2/3*F31/3 ~=
1.04*ε2/3*F31/3.
 |
The second derivative
We obtain in a similar way the error in estimating the second derivative of f(x), the optimal value of
Δx:
optim Δx = (48*ε/F4)1/4
and the minimum error:
minimum Error = ((1/12)*481/2+4*48−1/2)*ε1/2*
F41/2 ~= 1.15*(ε*F4)1/2.
(2)
Estimates F3 and F4< of the third and fourth derivatives are respectively:
F3 ≈ (f(x+2*Δx)−2·f(x+Δx)+2*f(x−Δx)−
f(x−2*Δx) )/(2*Δx3);
F4 ≈ (f(x+2*Δx)−4·f(x+Δx)+6*f(x)−
4*f(x−Δx)+f(x−2*Δx) )/Δx4.
(3)
Limits of the accuracy of the curvature
A modest demand:
the curvature error ≤10%;
coordinate error ε= 0.7 pixel |
 |
Consider a coordinate system, whose X-axis is the tangent to the curve at the point with a given x, and the
Y-axis is the normal of the curve at x. Then C =
d 2y/dx2 and we can apply the equation (2) to estimate
the error of C. Suppose the curve has F4 of the same order of magnitude as a circle of the same curvature,
i.e. F4 ≈ 3*C3;
dC/C = 1.15*(0.7*3*C3)1/2/C ≤ 0.1, which implies
C≤0.0036 pixel-1
and corresponds to R≥277 pixels.
This value corresponds to optimal Δx = (48*0.7/3)1/4*C-3/4 = 125
pixels and an arc of 53 degrees.
For curves with smaller radii the error is >> 10%.
For instance, for R = 16 pixels (i.e.C = 1/16 ~= 0.063) and
F4=3·C3 the error is equal to
1.15*sqrt(0.7*3*16-3) ≈ 0.024; the relative error ≥ 38%.
Optimal Δx = (48·0.7·R3/3)1/4 ~= 15 pixels, chord length of 30
pixels, arc = 142 degrees.
This means that to estimate the curvature with a precision of 10% we should investigate pieces of the curve of a length of 125 pixels
corresponding to an arc of 53 degrees which is too coarse.
Conclusion: ε=0.7 pixels and error ≤10% imply R≥277 pixels,
arc ≥53 degrees.which is too coarse.
We suggest to use a gray value image instead of a binary image and to estimate the coordinates of the points of the curve with a
sub-pixel precision.Then we can have a coordinate error of about 0.01 pixel and use much smaller values of Δx
See the lecture "Sub-pixel estimation of curvature".
Download: Print version
Let me know